V6 Vector equation of a line
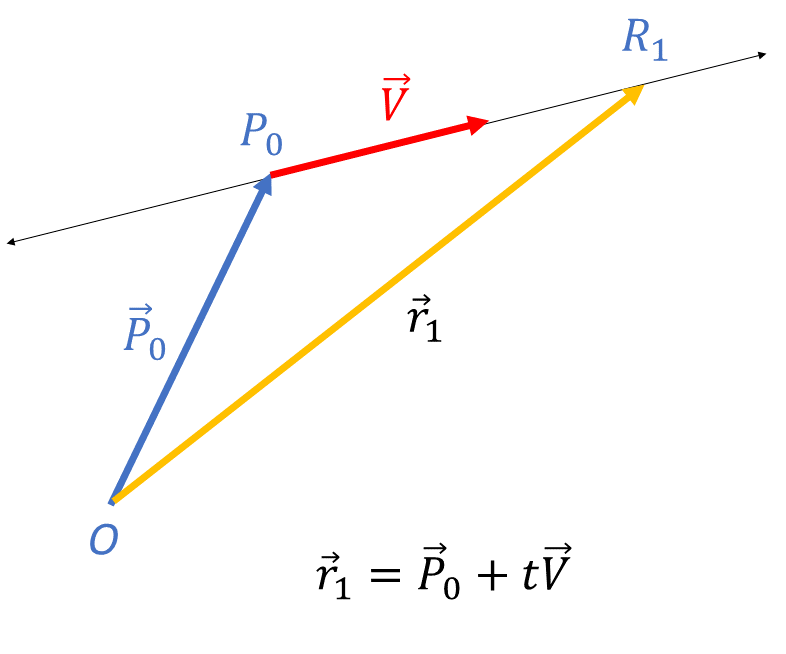
If you want to uniquely define a line, you need to pin it between two points in 3-dimensional space. You can also define a point with a 3-dimensional vector through it. This process uses three types of equations.
Learn how to find the vector equation, the parametric equation, and the symmetric equation of a line in three-dimensional space.
Introduction
You have probably been taught that a line in the \(x-y\) plane can be represented in the form \[\begin{align*} y & =mx+c \end{align*}\] where \(m\) is the gradient ( or slope) of the line and \(c\) is the \(y-\)intercept. But how do we define a line in three dimensions (3D)? 1 Three dimensional space (3D) is a geometric setting in which three co-ordinates are required to determine the position of a point. This is different to when we are dealing with points in the \(x-y\) plane where only two co-ordinates are required.
This module deals with the equation of a line in 3D.
Vector Equation of a Line in 3D
A line in 3D space can be described by a point and a vector along the line. There is only one line that can be drawn through a given point in the direction of a given vector.
Consider the figure below:
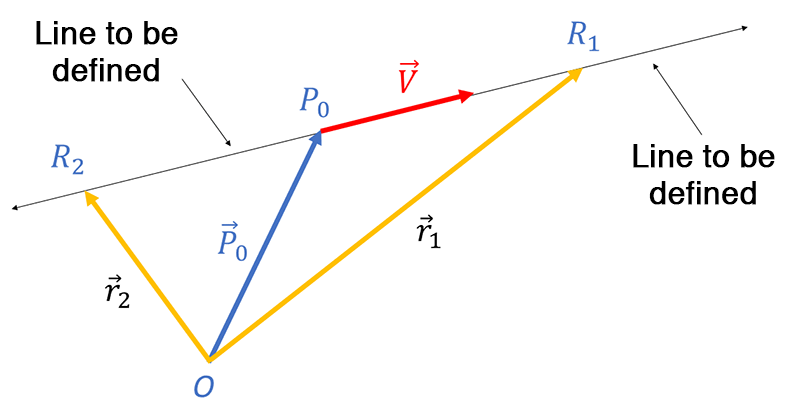
Here
\(\vec{r_{1}}\) and \(\vec{r}_{2}\) are two points on the line;
\(P_{0}\left(x,y,z\right)\) is a point on the line and \(\vec{P}_{0}\) is it’s position vector;
\(\vec{V}\) is a vector along the line;
\(t\) is a constant. That is \(t\in\mathbb{R}\). To get to the point \(R_{1}\) you first need to get onto the line. You do this by traveling along \(\vec{P}_{0}\) to the point \(P_{0}\) on the line and then traveling a distance along the line in the direction of vector \(\vec{V}\) . So we could write \[\begin{align*} \vec{r}_{1} & =\vec{P}_{0}+t\vec{V} \end{align*}\] where \(t\) is a positive constant. The quantity \(t\vec{V}\) represents the distance and the direction we need to go along the line to get to the point \(R_{1}\) from \(P_{0}\) .
To get to the point \(R_{2}\) you first need to get onto the line. You do this by traveling along \(\vec{P}_{0}\) to the point \(P_{0}\) on the line and then traveling a distance along the line in the opposite direction of vector \(\vec{V}\) . So we could write \[\begin{align*} \vec{r}_{1} & =\vec{P}_{0}+t\vec{V} \end{align*}\] where \(t\) is a negative constant (because we are going in the direction opposite to \(\vec{V}\)).
Considering the above, we hope you understand the equation of a line, in vector form, is \[\begin{align*} \vec{r} & =\vec{P_{0}}+t\vec{V} & \left(1\right) \end{align*}\] where \(t\in\mathbb{R}\) is a constant.
It is also possible to define the line in other forms as described below.
Parametric Equation of a Line in 3D
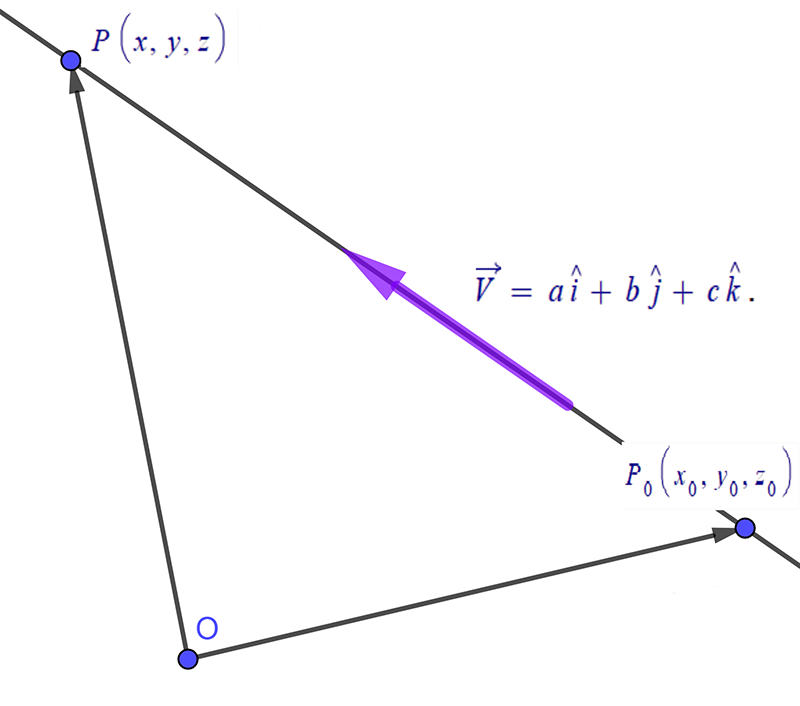
Suppose we wish to find the line that goes through the point \(P_{0}\left(x_{0},y_{0},z_{0}\right)\) in the direction of the vector \(\overrightarrow{V}=a\hat{i}+b\hat{j}+c\hat{k}\) . Consider a general point \(P\left(x,y,z\right)\) that lies on the line that goes through the point \(P_{0}\left(x_{0},y_{0},z_{0}\right)\) as shown at right. We can define a vector \(\overrightarrow{P_{0}P}\) by:
\[\begin{align*} \overrightarrow{P_{0}P} & =\left(x-x_{0}\right)\hat{i}+\left(y-y_{0}\right)\hat{j}+\left(z-z_{0}\right)\hat{k}. & \left(2\right) \end{align*}\]
This vector will obviously be in the same direction as \(\overrightarrow{V}\) but will, in all likelihood have a different magnitude. In other words \(\overrightarrow{P_{0}P}\) will be a multiple of the direction vector \(\overrightarrow{V}.\) So \(\overrightarrow{P_{0}P}=t\overrightarrow{V}\) where \(t\in\mathbb{R}\) is some number.
Hence:
\[\begin{alignat*}{2} \overrightarrow{P_{0}P} & =t\overrightarrow{V}\\ & =t\left(a\hat{i}+b\hat{j}+c\hat{k}\right)\\ & =at\hat{i}+bt\hat{j}+ct\hat{k}. & \left(3\right) \end{alignat*}\]
Equating components of \(\left(2\right)\) and \(\left(3\right)\) we have, \[\begin{align*} \left(x-x_{0}\right) & =at\\ x & =x_{0}+at & \left(4\right) \end{align*}\]
and
\[\begin{align*} \left(y-y_{0}\right) & =bt\\ y & =y_{0}+bt & \left(5\right) \end{align*}\]
and
\[\begin{align*} \left(z-z_{0}\right) & =ct\\ z & =z_{0}+ct. & \left(6\right) \end{align*}\]
These equations \(x=x_{0}+at\), \(y=y_{0}+bt\) and \(z=z_{0}+ct\) are called the parametric equations of the line that contains the point \(\left(x_{0},y_{0},z_{0}\right)\) and has the direction vector \(\overrightarrow{V}=a\hat{i}+b\hat{j}+c\hat{k}\). The variable \(t\in\mathbb{R}\) is called a parameter.
Symmetric Form of the Line
By rearranging \(\left(4\right)\) to \(\left(6\right)\) above we find: \[\begin{align*} t & =\frac{x-x_{0}}{a}\\ t & =\frac{y-y_{0}}{b}\\ t & =\frac{z-z_{0}}{c}. \end{align*}\]
Since they are all equal, we can say that:
\[\begin{align*} \frac{x-x_{0}}{a} & =\frac{y-y_{0}}{b}=\frac{z-z_{0}}{c} & \left(7\right) \end{align*}\]
This is called the symmetric form of the equation of the line.
Summary
A line in 3D may be represented:
In vector form (see \(\left(1\right)\) above)
In parametric form (see \(\left(4-6\right)\) above)
In symmetric form (see \(\left(7\right)\)above).
Example \(1\)
Find the parametric and symmetric equations of the line that goes through the point \((3,2,3)\) and is in the direction of the vector \(2\hat{i}+\hat{j}-5\hat{k}\) .
Solution:
Using equations \(\left(4-6\right)\) the parametric equations will be :
\[\begin{align*} x & =3+2t\\ y & =2+t\\ z & =3-5t. \end{align*}\]
Using equation \(\left(7\right)\) the symmetric equations will be: \[\begin{alignat*}{1} \frac{x-3}{2} & =\frac{y-2}{1}=\frac{z-3}{-5} \end{alignat*}\]
or
\[\begin{alignat*}{1} \frac{x-3}{2} & =y-2=\frac{3-z}{5}. \end{alignat*}\]
Example \(2\)
Find the parametric and symmetric equations of the line that goes through the point \((1,3,2)\) in the direction of the vector \(\overrightarrow{V}=\hat{j}-2\hat{k}\) .
Solution:
The parametric equations will be:
\[\begin{align*} x & =1+0t\\ & =1\\ y & =3+t\\ z & =2-2t. \end{align*}\]
The symmetric equation will be: \[\begin{align*} x=1 & ;\,y-3=\frac{z-2}{-2} \end{align*}\]
or
\[\begin{align*} x=1 & ;\,y-3=-\frac{1}{2}z+1. \end{align*}\]
Example \(3\)
Find the direction vector of the line : \[\begin{align*} \frac{x-6}{2} & =\frac{y-2}{-1}=\frac{z}{3}. \end{align*}\]
Solution:
The line is in symmetric form and so \[\begin{align*} \frac{x-6}{2} & =t\\ \frac{y-2}{-1} & =t\\ \frac{z}{3} & =t \end{align*}\] for any \(t\in\mathbb{R}.\) Rearranging gives the parametric form:
\[\begin{align*} x & =6+2t\\ y & =2-t\\ z & =3t. \end{align*}\] This may be written in vector form as \[\begin{align*} x\hat{i}+y\hat{j}+z\hat{k} & =\left(6\hat{i}+2\hat{j}+0\hat{k}\right)+t\left(2\hat{i}-\hat{j}+3\hat{k}\right) \end{align*}\] which is a line through the point \(\left(6,2,0\right)\) in the direction \(\left(2\hat{i}-\hat{j}+3\hat{k}\right)\).
Hence the direction vector is \(\overrightarrow{V}=2\hat{i}-\hat{j}+3\hat{k}\). Note that the direction vector of the line could be any multiple of this vector.
Example 4
A line passes through the points \(A(1,2,4)\) and \(B(3,-1,-2)\). Find the equation of the line in a) vector format b) in parametric format and c) in symmetric format.
Solution:
- For vector format we need to find a vector along the line. This can be
2 Note that it is also valid to take the vector \(\overrightarrow{BA}\).\[\begin{alignat*}{1} \overrightarrow{AB} & =\left(3-1\right)\hat{i}+\left(-1-2\right)\hat{j}+\left(-2-4\right)\hat{k}\\ & =2\hat{i}-3\hat{j}-6\hat{k} \end{alignat*}\]
The vector \(\overrightarrow{AB}\) is the direction vector along the line. We can now use either point, \(A\) or \(B\) to find the equation of the line in vector format. So the possible vector forms are:
\[\begin{align*} \vec{r} & =\left(\hat{i}+2\hat{j}+4\hat{k}\right)+t\left(2\hat{i}-3\hat{j}-6\hat{k}\right) & \left(8\right) \end{align*}\] where \(t\in\mathbb{R}\) and we have used point \(A\), or \[\begin{align*} \vec{r} & =\left(3\hat{i}-\hat{j}-2\hat{k}\right)+t\left(2\hat{i}-3\hat{j}-6\hat{k}\right) & \left(9\right) \end{align*}\] where we have used point \(B\). Either is acceptable.
- For the parametric equations, you can use either \(\left(8\right)\) or \(\left(9\right)\). We will use \(\left(8\right)\).
Equating components, we have
3 Remember \[\begin{align*} \vec{r} & =x\hat{i}+y\hat{j}+z\hat{k} \end{align*}\] where \(x,\) \(y\) and \(z\) are the coordinates of any point on the line. \[\begin{align*} \vec{r} & =\left(1\hat{i}+2\hat{j}+4\hat{k}\right)+t\left(2\hat{i}-3\hat{j}-6\hat{k}\right)\\ x\hat{i}+y\hat{j}+z\hat{k} & =\left(1\hat{i}+2\hat{j}+4\hat{k}\right)+t\left(2\hat{i}-3\hat{j}-6\hat{k}\right) \end{align*}\] and so the parametric equations are \[\begin{align*} x & =1+2t & \left(10\right)\\ y & =2-3t & \left(11\right)\\ z & =4-6t & \left(12\right) \end{align*}\] are the parametric equations.
- The symmetric equations are obtained by solving \(\left(10-12\right)\) for \(t\) to get
\[\begin{align*} t & =\frac{x-1}{2}\\ t & =\frac{2-y}{3}\\ t & =\frac{4-z}{6}. \end{align*}\]
So the symmetric equations are: \[\begin{alignat*}{1} \frac{x-1}{2} & =\frac{2-y}{3}=\frac{4-z}{6}. \end{alignat*}\]
Note that you will get different parametric and symmetric equations if you use \(\left(9\right)\) above. However they are acceptable solutions.
Exercise:
Find the symmetric and parametric equations of the lines that satisfy the given conditions:
Contains the point \(\left(1,-1,2\right)\) with the direction vector \(2\hat{i}-2\hat{j}+3\hat{k}\,\)?
Answer: \(\frac{x-1}{2}=\frac{y+1}{-2}=\frac{z-2}{3}\) and \(x=1+2t\) ; \(y=-1-2t\) ; \(z=2+3t\)Contains the point \(\left(3,4,-1\right)\) with the direction vector \(\hat{i}+\hat{j}+5\hat{k}\,\)?
Answer: \(\frac{x-3}{1}=\frac{y-4}{1}=\frac{z+1}{5}\) and \(x=3+t\); \(y=4+t\); \(z=5t-1\)Contains the point \(\left(2,3,-1\right)\) parallel to \(\frac{x-1}{2}=\frac{y-3}{-1}=\frac{x+1}{3}\,\)?
Answer: \(\frac{x-2}{2}=\frac{y-3}{-1}=\frac{z+1}{3}\) and \(x=2+2t\) ; \(y=3-t\) ; \(z=-1+3t\)Contains the point \(\left(2,2,1\right)\) and \(\left(1,1,3\right)\,\)?
Answer: \(\frac{x-1}{1}=\frac{y-1}{1}=\frac{z-3}{-2}\) and \(x=1+t\); \(y=1+t\); \(z=3-2t\)
or
\(\frac{x-2}{1}=\frac{y-2}{1}=\frac{z-1}{-2}\text{ and $x=2+t;y=2+t;z=1-2t$ }\)
Download this page: V6 Vector Equation of a Line (PDF 300KB)
What's next... V7 Intersecting lines in 3D
